I modelli di ordine ridotto (ROM) sono uno strumento matematico sempre più importante per l’industria e l’ingegneria: riducendo i parametri di un sistema, permettono simulazioni in tempo reale in situazioni in cui sono necessarie numerose simulazioni per varie configurazioni di sistema, come ad esempio nella progettazione di vetture da Formula Uno o di eliche per navi. Questo è fondamentale per scenari che richiedono molteplici simulazioni sotto condizioni leggermente variabili o quando l'esecuzione di simulazioni a piena scala è impraticabile. Nonostante i vantaggi computazionali, questi metodi hanno difficoltà nel quantificare in modo affidabile l’incertezza dei modelli stessi e delle simulazioni, il che rende difficile la loro integrazione in pipeline industriali.
Un recente studio SISSA, pubblicato su Nature Scientific Reports, propone un nuovo approccio, battezzato GAROM, per simulare sistemi fisici complessi combinando l’intelligenza artificiale con i metodi di ordine ridotto, per creare un nuovo tipo di modelli in grado di quantificare l’incertezza associata, e quindi “riconoscere” quando commettono errori.
“L'approccio si basa sull'uso di due reti neurali: il generatore, che produce risultati di simulazione con relative incertezze, e il discriminatore, che cerca di distinguere se i dati in ingresso provengono da una simulazione o sono stati generati” spiega Dario Coscia di SISSA mathLab, il laboratorio di modellistica matematica e calcolo scientifico della SISSA, primo autore della ricerca . “L'obiettivo è che il generatore inganni il discriminatore, mentre quest'ultimo cerca di diventare sempre più accurato nel riconoscere le simulazioni genuine.“
Questo processo di addestramento di due reti neurali in competizione tra loro (Generative Adversarial Networks, GAN) è stato combinato ai modelli di ordine ridotto (Reduced Order Models, o ROM), per creare GAROM, riducendo i costi computazionali come per i ROM più “tradizionali”, ma con vantaggi aggiuntivi rispetto a entrambi gli approcci.
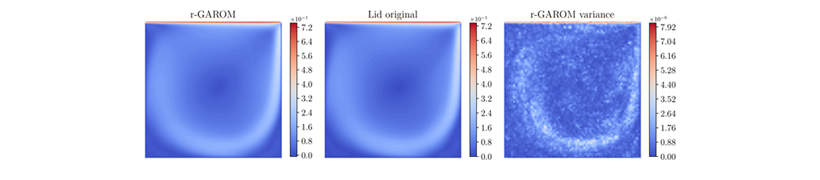
Nell’articolo si mostra come GAROM può essere applicato a problemi complessi di fluidodinamica, una disciplina fondamentale per applicazioni in settori come l’aeronautica, il navale, la medicina e la meteorologia. I risultati sono paragonabili o addirittura superiori allo stato dell’arte ma con l’aggiunta cruciale della quantificazione dell’incertezza, ovviando a uno dei problemi più comuni dei modelli ridotti Data-Driven.

